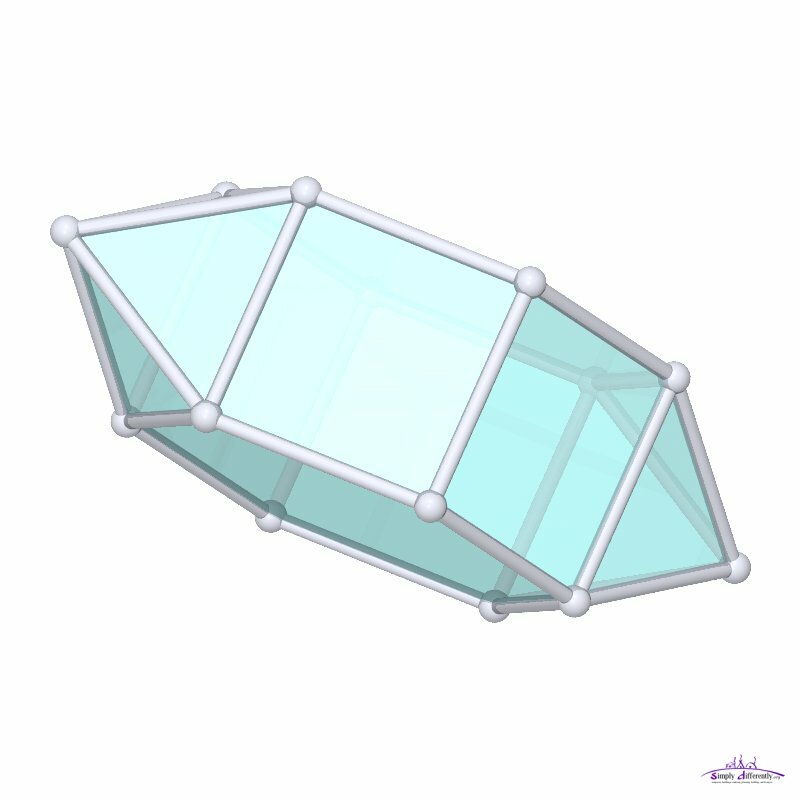
Welcome to “How Many Faces, Edges, and Vertices Does a Pentagonal Prism Have?” with Mr. J! Need help with faces, edges and vertices? You’re in the right plac.. In mathematics, a pentagonal prism is a three-dimensional geometric figure that has five lateral rectangular faces with two congruent and parallel pentagonal bases. A pentagonal prism is a type of heptahedron that belongs to the polyhedron family, which has seven plane faces. It has seven faces, ten vertices, and fifteen edges.

Pentagonal prism cargaret

Pentagonal Prism Definition, Formulae of Volume & Surface Area, Examples

Pentagonal Prism Definition, Formulae of Volume & Surface Area, Examples
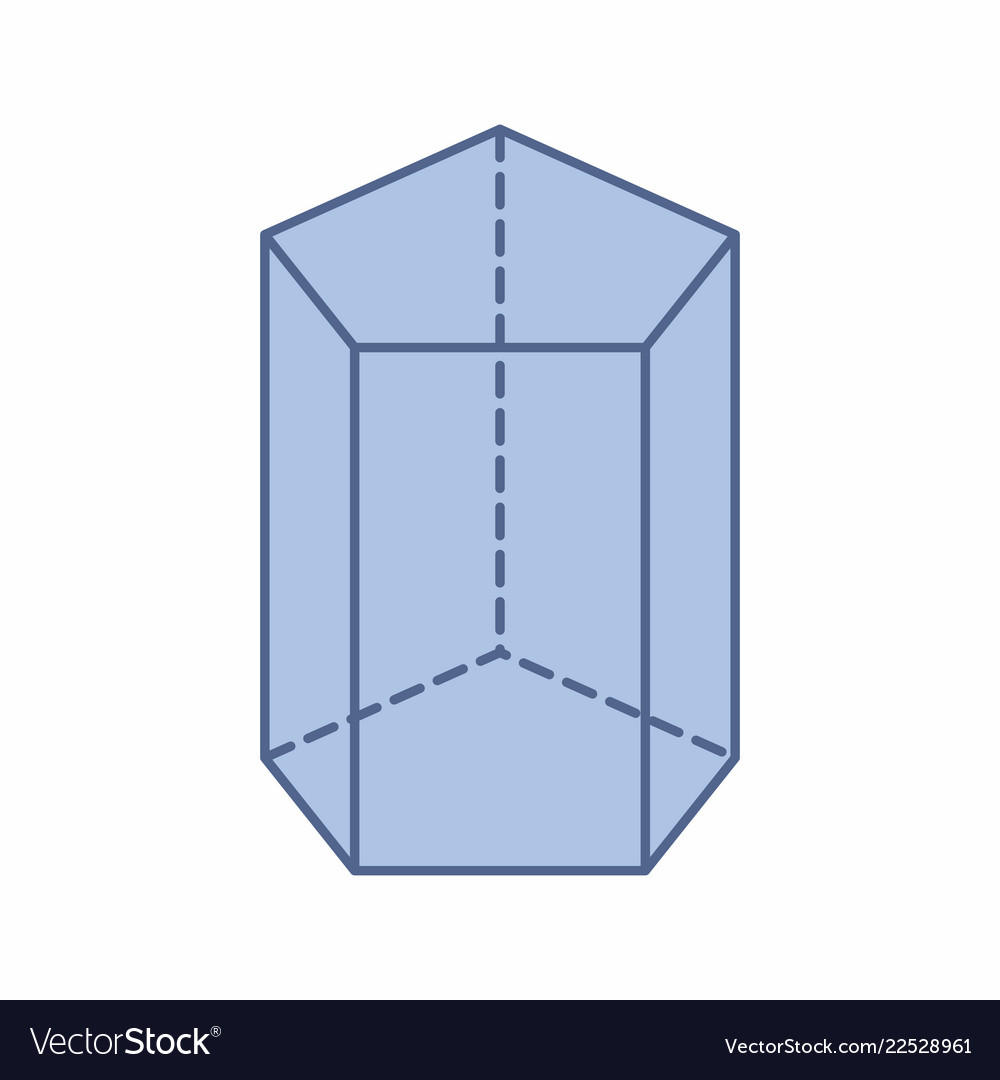
Pentagonal prism Royalty Free Vector Image VectorStock

Pentagonal Prism Definition, Formulae of Volume & Surface Area, Examples
Pentagonal Pyramid ClipArt ETC

How Many Faces, Edges, and Vertices Does a Pentagonal Prism Have? Geometry Math with Mr. J
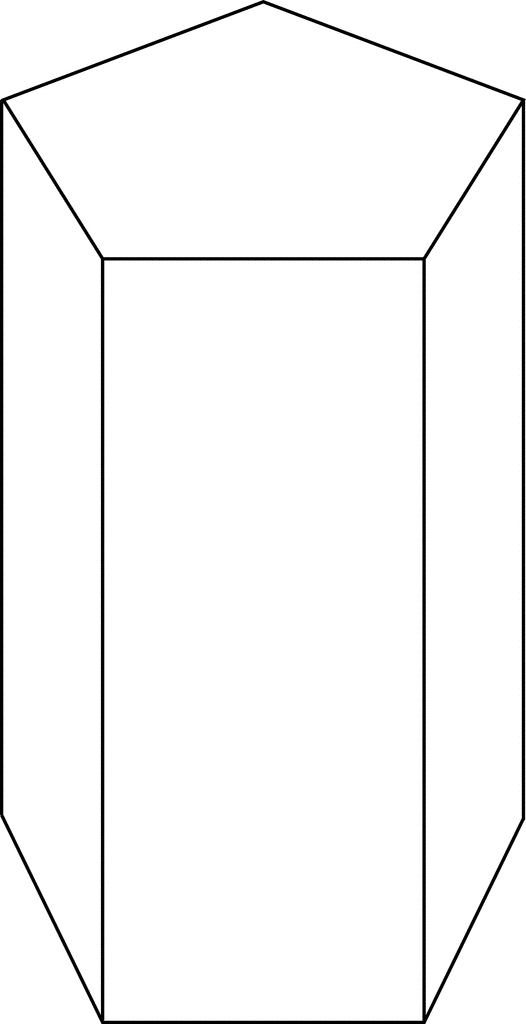
Pentagonal Prism ClipArt ETC
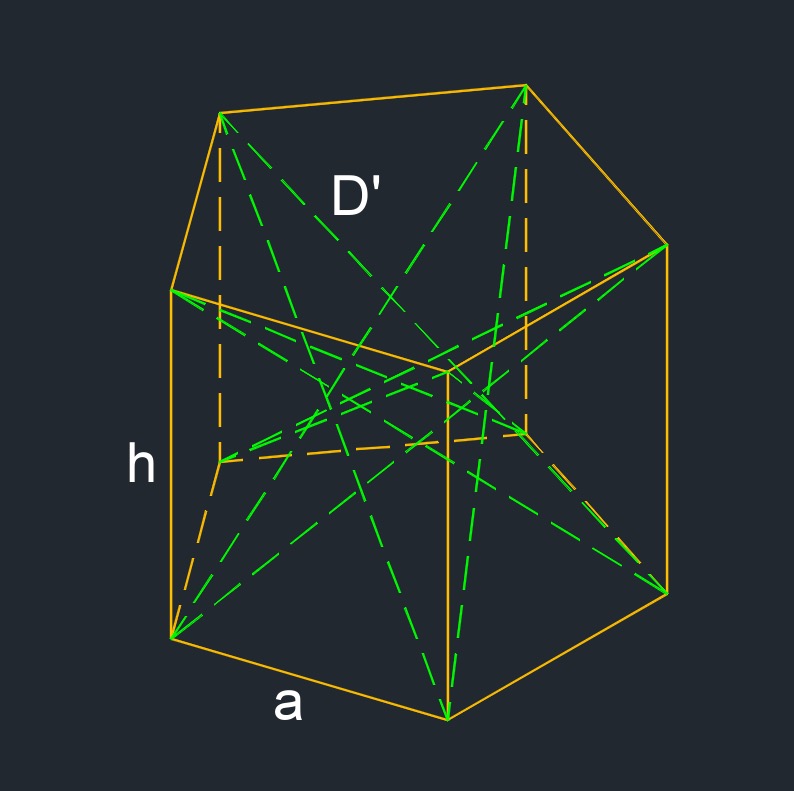
Pentagonal Prism Formulas Examples And Diagram vrogue.co
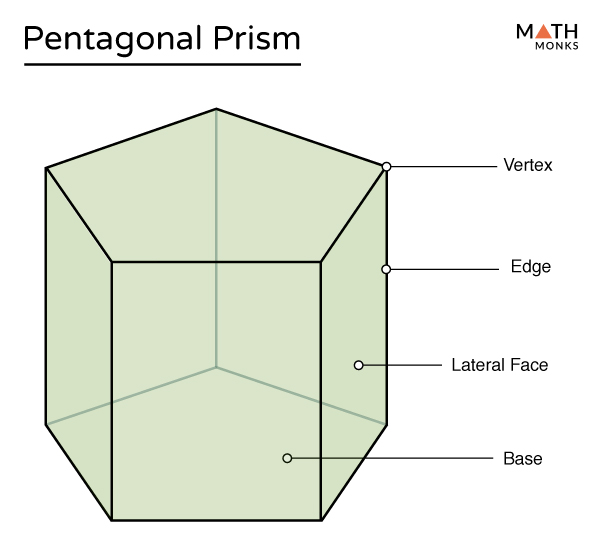
Pentagonal Prism Formulas, Examples and Diagram

Pentagonal Prism Edges The Pentagonal Prism As the name suggests, it is a prism based on a

Pentagonal Prism Cuemath
Jojo Bentley How Many Vertices Does Pentagonal Prism Have / A pentagonal prism has 7 faces How

isometric projection of a pentagonal prism YouTube

Pentagonal Prism Cuemath

Pentagonal Prism Cuemath

How many edges does a pentagonal prism has ? CLASS 6 UNDERSTANDING ELEMENTARY SHAPES MAT
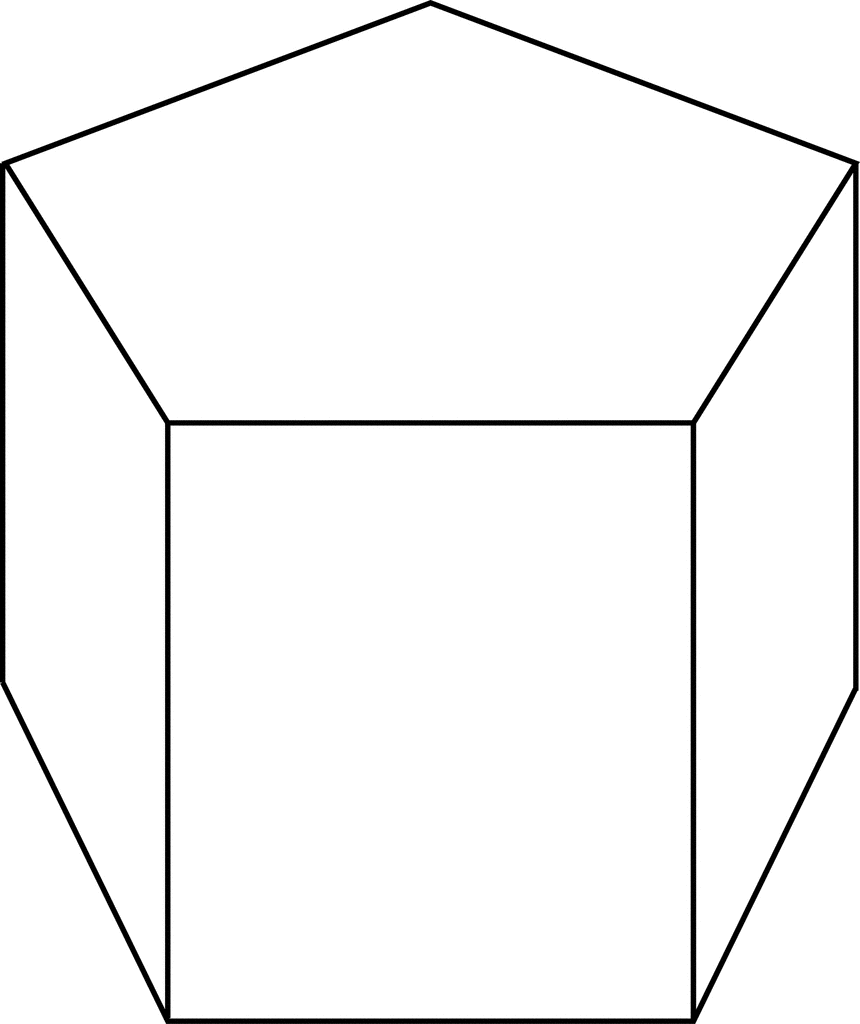
Pentagonal Prism ClipArt ETC
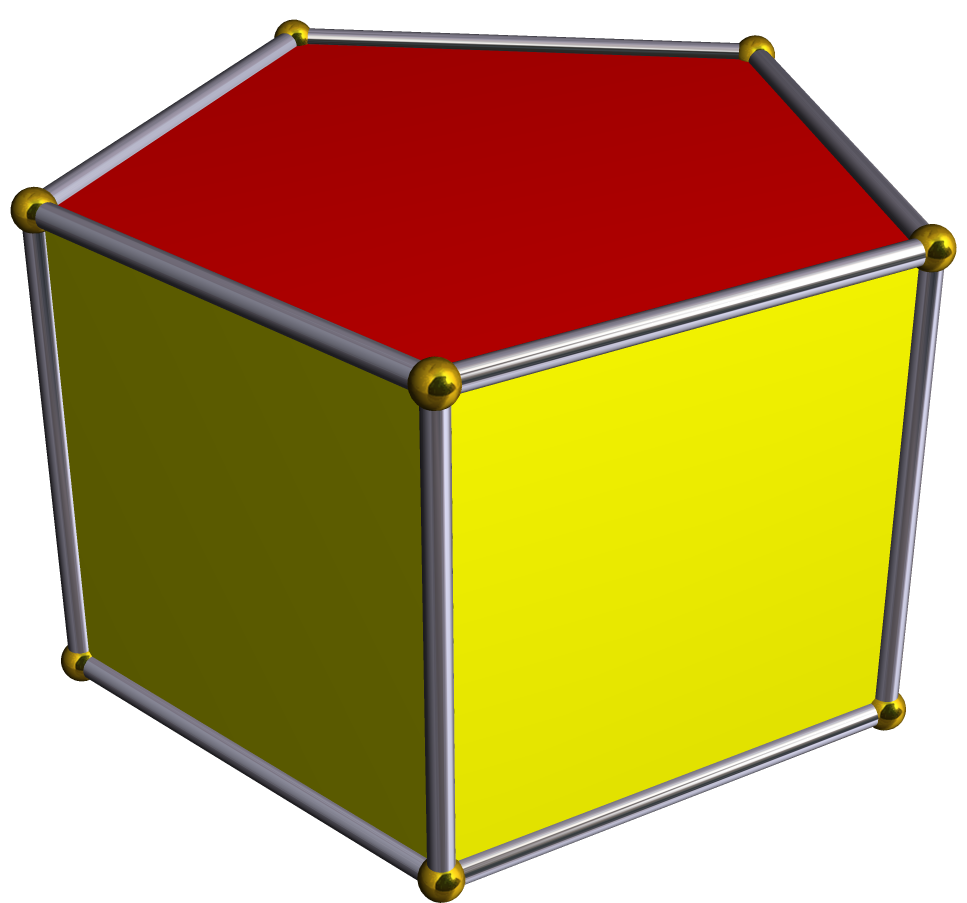
Prism Math Wiki

Pentagonal Prism Faces Edges And Vertices
Solution: To calculate the volume of a regular pentagonal prism, we use the formula below: V = 5 / 2 × a × b × h. Plugging the values in the formula for the surface area of a regular pentagonal prism, we get. V = 5 / 2 × 10 × 20 × 15 = 7500 cubic cm. Thus, the volume of the chocolate box is 7500 cubic cm.. Pentagonal prism as a semiregular (or uniform) polyhedron. If faces are all regular, the pentagonal prism is a semiregular polyhedron, more generally, a uniform polyhedron, and the third in an infinite set of prisms formed by square sides and two regular polygon caps. It can be seen as a truncated pentagonal hosohedron, represented by Schläfli.

