wherever the limit exists is defined to be the derivative of f at x and is denoted by f ′ ( x). This definition of derivative is called the first principle of differentiation. ∴ f ′ ( x) = lim h → 0. . f ( x + h) – f ( x) h. There are different notations for derivative of a function. Sometimes f ′ ( x) is denoted by d d x ( f ( x.. Derivative by first principle refers to using algebra to find a general expression for the slope of a curve. It is also known as the delta method.. The above examples demonstrate the method by which the derivative is computed.. ( x=1 \) is most likely to come when we differentiate the given expression and put one of the variables to be.

SPM (Add Maths) Differentiation by First Principle Rule YouTube

Differentiation by First Principle All Formulae of Differentiation YouTube

Example 19 Find derivative from first principle f(x) = (2x + 3)/(x

First Principle Differentiation Calculator
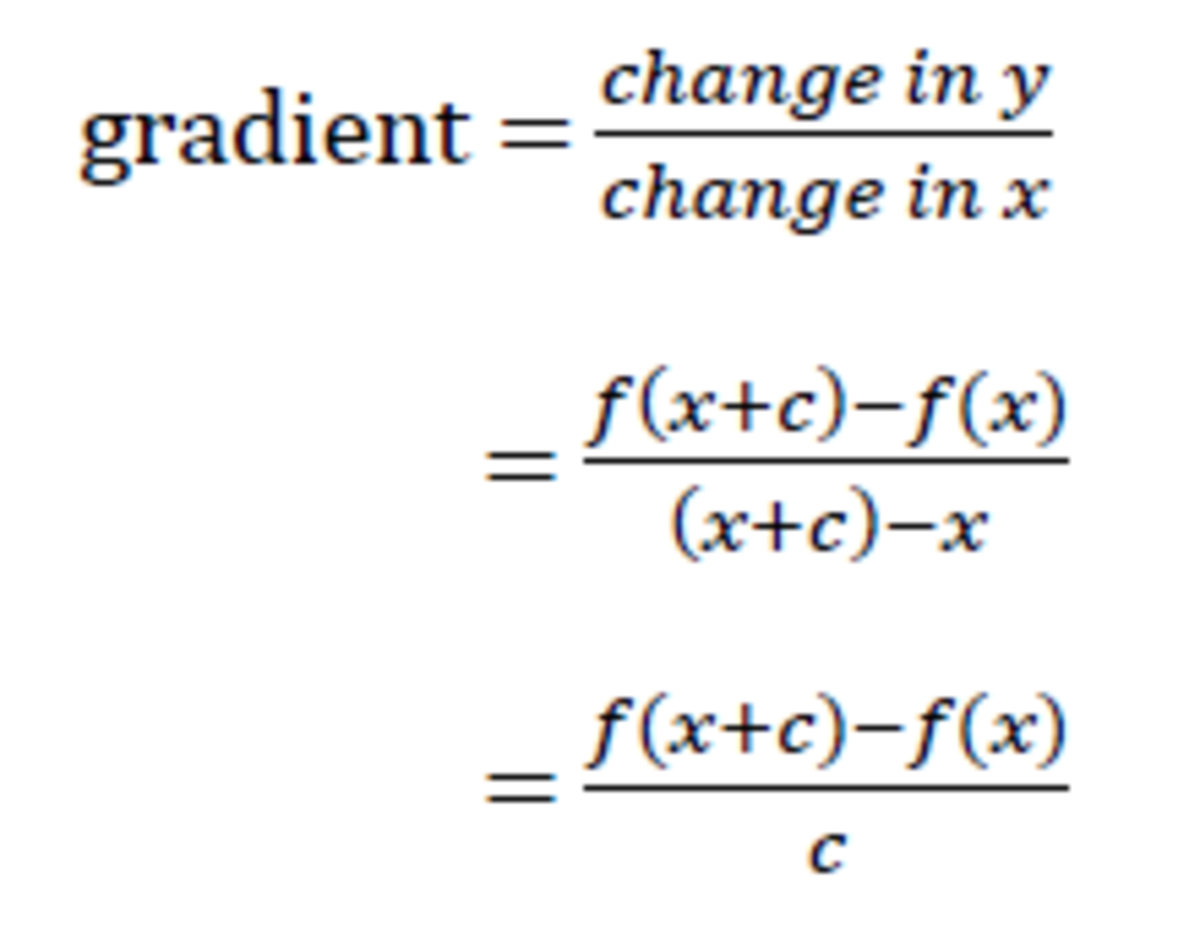
How to Differentiate From First Principles Owlcation

How To Differentiate x^3 From First Principles YouTube
![[Solved] Differentation from first principles apparent](https://i.stack.imgur.com/JLC0H.png)
[Solved] Differentation from first principles apparent 9to5Science

How to Differentiate by First Principles

Example 19 Find derivative from first principle Class 11

How to Find the Derivative of x^2 from First Principles YouTube

How to Differentiate by First Principles

DIFFERENTIATION FROM FIRST PRINCIPLE TRIG EXAMPLE YouTube

Differentiation from First Principles a simple explanation of how it works YouTube

How to Find the Derivative of a^x from First Principles YouTube

Differentiation B Differentiation from First Principles 2 YouTube

More examples of differentiating from first principles. YouTube
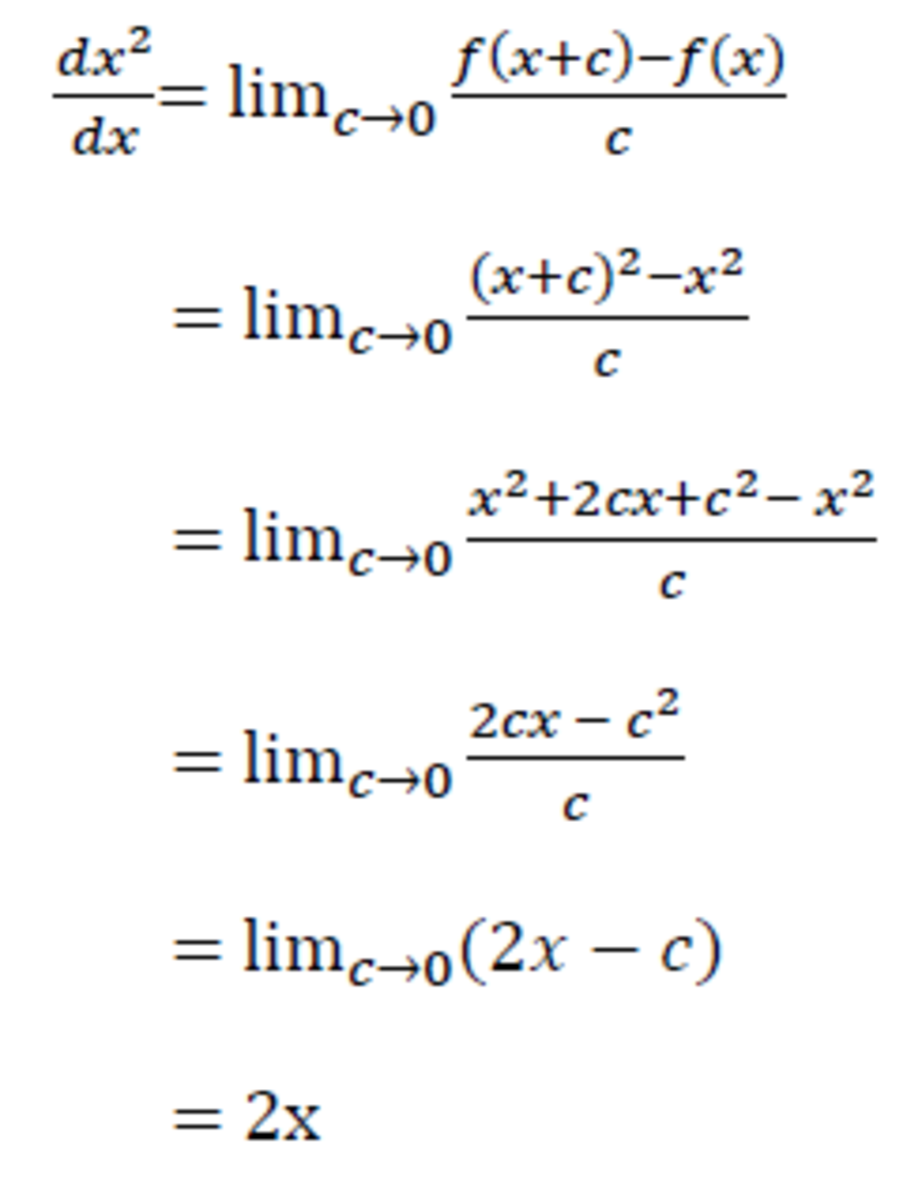
How to Differentiate From First Principles Owlcation

Differentiation from First Principles YouTube
Math12 CHAPTER 2 DIFFERENTIATION

ten Differentiation from first principles YouTube
6.2 Differentiation from first principles (EMCH6) We know that the gradient of the tangent to a curve with equation \ (y = f (x)\) at \ (x=a\) can be determine using the formula: We can use this formula to determine an expression that describes the gradient of the graph (or the gradient of the tangent to the graph) at any point on the graph.. Figure 1. A graph of the straight line y = 3x + 2. We can calculate the gradient of this line as follows. We take two points and calculate the change in y divided by the change in x. When x changes from −1 to 0, y changes from −1 to 2, and so. the gradient =. 2 − (−1) 3. =. 0 − (−1) 1.

